Proving A Triangle Is Isosceles
Proofs involving isosceles triangles oftentimes require special consideration considering an isosceles triangle has several distinct properties that do not utilise to normal triangles.(More about triangle types) Therefore, when you are trying to prove that 2 triangles are congruent, and one or both triangles, are isosceles you have a few theorems that you tin use to make your life easier.
Isosceles Triangle
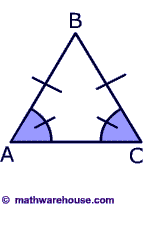
An isosceles triangle has ii congruent sides and 2 congruent angles. The coinciding angles are called the base angles and the other angle is known as the vertex angle. $$ \bending $$BAC and $$ \bending $$BCA are the base angles of the triangle movie on the left. The vertex angle is $$ \bending $$ABC
Isosceles Triangle Theorems
The Base Angles Theorem
If ii sides of a triangle are congruent, then the angles opposite those sides are coinciding.
Converse of the Base of operations Angles Theorem
The converse of the base angles theorem, states that if two angles of a triangle are congruent, then sides opposite those angles are congruent.
Proof 1
Proof 2
- Theorems and Postulates for proving triangles congruent
- Hypotenuse Leg Theorem
- Side Side Side
- Side Angle Side
- Bending Side Bending
- Angle Angle Side
- isosceles triangle proofs
- CPCTC
- indirect proof
- quiz on all theorems/postulates
- Images
- Free Math Printable Worksheets
- Worksheets & Activities on Triangle Proofs
Proving A Triangle Is Isosceles,
Source: https://www.mathwarehouse.com/geometry/congruent_triangles/isosceles-triangle-theorems-proofs.php
Posted by: kongnoestringthe.blogspot.com
0 Response to "Proving A Triangle Is Isosceles"
Post a Comment