Vertical Line Test Math Definition
Ray is a licensed engineer in the Philippines. He loves to write most mathematics and civil engineering.
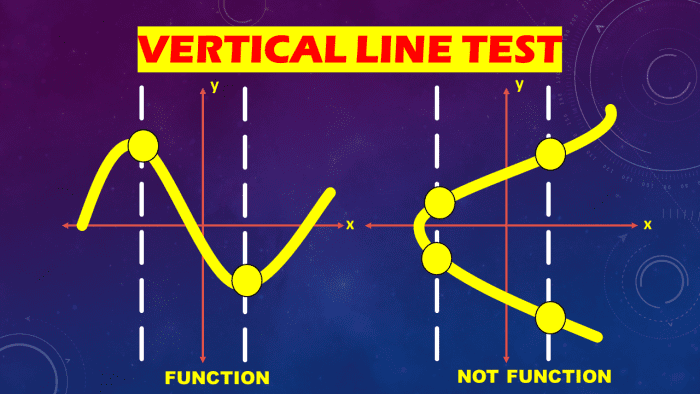
Vertical Line Test Definition
What Is the Vertical Line Test?
The vertical line test is a graphical test method used to determine whether a graph is the graph of a function. The vertical line test states that the graph of a prepare of points in a coordinate aeroplane is the function'south graph if every vertical line intersects the graph in at most one signal.
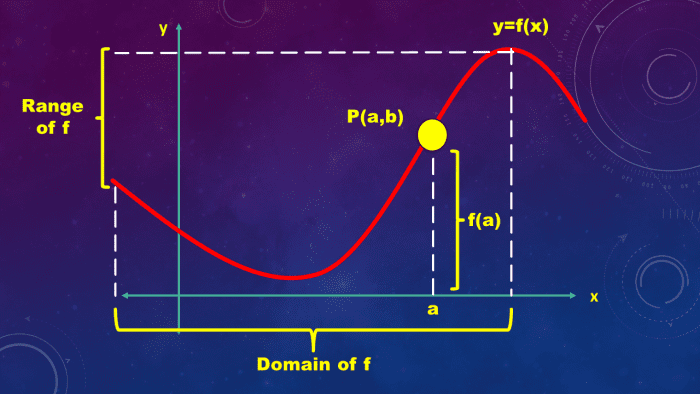
Nosotros frequently adhere the label y = f(10) to a sketch of the graph. If P(a,b) is a point on the function's graph, y-coordinate b is the function value f(a), as illustrated in the figure below. The figure shows the function f'southward domain, which is the set of possible values of x, and the range, which is the respective values of y. Although the domain and range are closed intervals, they may exist infinite intervals or other sets of real numbers.
Since there is exactly i value f(a) for each variable "a" in the domain of function f, but one point on the graph of f has x-coordinate a. In full general, we may apply the vertical line test to identify functions. Thus, every vertical line intersects the graph of a function at most one signal.
Consequently, the graph of a office cannot be a figure such as a circle or an ellipse, in which a vertical line may intersect the graph at more than than one point. The x-intercepts of the graph of a part f are the solutions of the equation f(10) = 0. These numbers are called the zeros of the function. The y-intercept of the graph is f(0) if information technology exists.
Vertical Line Examination Function
How to Perform Vertical Line Test
The vertical line exam is a simple method to decide if a curve is a function graph or non. Find from the figure shown beneath. The vertical line test is helpful for graphical purposes only. In unproblematic terms, information technology is a visual way to check if a curve is a graph of a function. Take note that the vertical line test shall laissez passer the post-obit:
- The graph shall only have one output of y for every input of x.
- Depict a vertical line and check if it intersects a curve on an XY plane more than than once. If so, the curve is not a office graph and therefore does not correspond a role. This status causes the relationship to be not qualified. Otherwise, if all drawn vertical lines intersect the curve at most one time, it ways the graph is a function.
Case 1: Identifying if a Given Equation Is a Role
Graph the line with an equation yii = -5x and show it is a function.
Solution
By observing the equation itself, nosotros can infer that the graph of the function is a parabola opening to the left. At present, to brand certain of it, allow us solve for the values of y-values for some x-values. Try to substitute x = 0, 10 = -5, x = -10, ten = -25, and ten = -xl.
| x-values | y-values |
|---|---|
| 0 | 0 |
| -5 | 5, -5 |
| -ten | five√2, -five√two |
| -25 | 5√5, -5√5 |
| -forty | 10√two, -10√two |
And so, draw a vertical line across the sketch of the graph using the obtained values of x and y. As y'all tin observe from the diagram shown below, the vertical line passes through two points. Therefore, the vertical line examination fails, and the line equation does not represent a function.
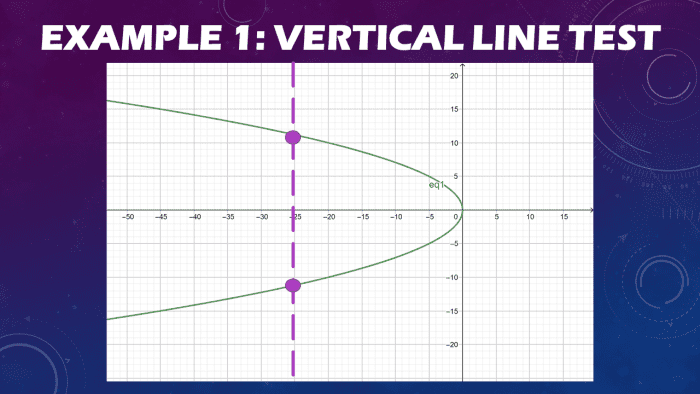
Identifying if a Given Equation Is a Office
Final Respond
Scroll to Go on
Read More than From Owlcation
The line y2 = -5x does non pass the vertical line examination and does non represent a function.
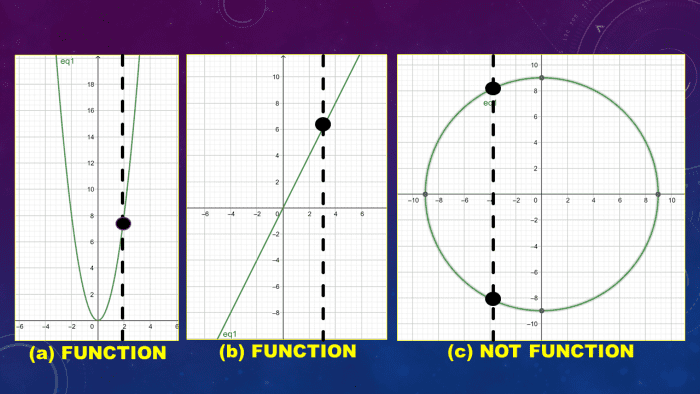
Example 2: Application of the Vertical Line Test
Which of the following graphs stand for a office y = f(x)?
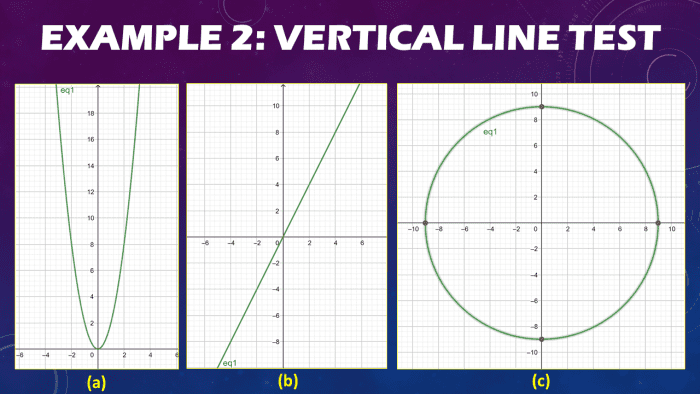
Application of the Vertical Line Test
Solution
There are three graphs of functions given that we demand to identify. Recall that the vertical line test states that if any vertical line intersects a graph more than once, the relation of the graphical sketch is not a function. Draw a vertical line on each of the diagrams and check how many points the vertical line intersects.
For (a), the graph sketched is a parabolic curve. Equally you tin observe from the vertical line passing through the function, there is only one point of intersection. Therefore, we tin conclude that the parabolic curve represents a function.
The same scenario applies for graph (b), as shown. The second graph is linear. Most linear graphs, when passing through a vertical line, satisfy the vertical line test. Therefore, the straight graph represents a role.
For graph (c), equally you lot can discover from the vertical line drawn across the sketch of the circular part, it passes through ii distinct points. No matter where yous put a vertical line, information technology passes through two points. Therefore, it does not arrange to the vertical line exam definition. At near x-values in the circle, information technology would intersect two or more y-values. Thus, the third graph does not represent a function.
Application of the Vertical Line Examination
Final Answer
Therefore, using the vertical line examination, the given parabolic graph and linear graph correspond a function, and the circular graph does not.
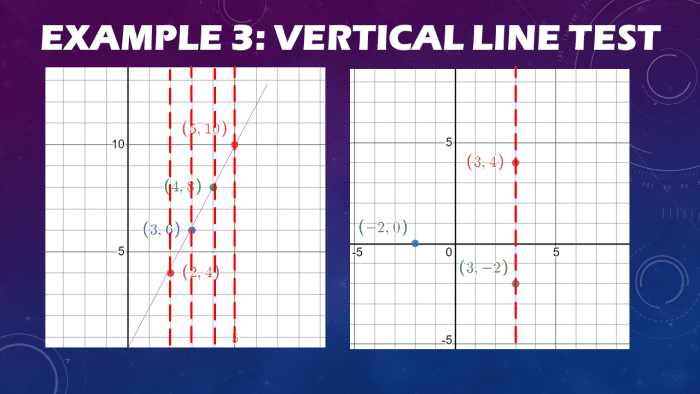
Case three: Identifying if a Relation Is a Function
Given the following relations, determine if they are functions using the vertical line test.
- A:{(2,4) (3,6) (four,8) (5,x)
- B:{(iii,4) (-2,0) (iii, -2)
Solution
The vertical line examination is easier to use given ordered pairs of a particular graph. It is a elementary plotting of the points in the cartesian coordinate organisation and checks if ordered pairs overlap vertically on the diagram. The primary consideration in this kind of vertical line test problem is to make sure the inputs are different, and the outputs tin be the aforementioned.
For the first ordered pairs A, we tin can see that no inputs are the same. Information technology means that vertical lines to pass through the graph of the given ordered pairs will pass through at precisely 1 point on the graphical sketch.
For function B, there are two ordered pairs with the same input of iii and have different ranges y. Therefore, this relation is non a part. Take a look at the graph of the given ordered pairs below.
Identifying if a Relation Is a Function
Terminal Answer
The relations A passes the vertical line exam and, therefore, a function. On the other hand, the ordered pair B is non a function since the vertical line exam fails and two of its pairs have the same inputs or x-values.
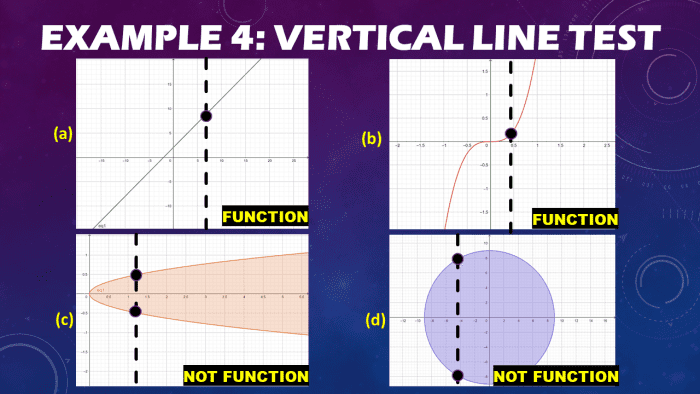
Case 4: Graphing Functions and Using the Vertical Line Examination
Graph the following lines and identify if they are functions using the vertical line test.
- f(x) = x + 2
- f(10) = 2x3
- x = 5y2
- x2 + yii = 81
Solution
In that location are two significant steps that you lot tin perform in determining if the given line equation represents a function. Outset, given the equation f(x), solve for y at whatsoever value of ten. Then, tabulate the results and graph them.
For f(x) = ten + ii, solve for the values of y at x = 0, x = i, x = -i, ten = v, and x = -5. Subsequently tabulating, plot the points in the cartesian coordinate airplane and perform the vertical line test.
| x-values | y-values |
|---|---|
| 0 | 2 |
| 1 | 3 |
| -one | ane |
| 5 | 7 |
| -5 | -3 |
Solve for the y-values of the cubic equation f(10) = 2x3 at 10 = 0, 10 = 1, ten = -ane, 10 = v, and x = -5. Plot the obtained points in the plane arrangement and practise the vertical line exam.
| x-values | y-values |
|---|---|
| 0 | 0 |
| 1 | 2 |
| -1 | -2 |
| 5 | 250 |
| -5 | -250 |
For the parabolic function x = 5ytwo, solve for the y-values for x = 0, x = 1, x = -one, ten = 5, and x = -5. Plot the points and graph the function. See if information technology passes the vertical line test.
| x-values | y-values |
|---|---|
| 0 | 0 |
| i | √five/five, -√5/5 |
| -i | √5i/5, -√5i/v |
| 5 | 1, -1 |
| -5 | i, -i |
Lastly, for the given equation x2 + y2 = 81, solve the y-values at x = 0, x = 1, x = -i, x = 9, and ten = -9. So, plot the points in the cartesian coordinate system and perform the vertical line test. Based on the obtained values, nosotros can easily infer that the equation does not represent a role considering of the recurring values on the column of y-values. Therefore, the pairs are unique for all x-values.
| 10-values | y-values |
|---|---|
| 0 | nine, -9 |
| 1 | 4√v, -4√5 |
| -one | 4√five, -4√5 |
| 9 | 0 |
| -9 | 0 |
Graphing Functions and Using the Vertical Line Examination
Terminal Reply
The graph of the equations f(10) = x + ii and f(x) = 2xthree laissez passer the vertical line test since the drawn vertical lines pass through only 1 betoken. A graph with i indicate of intersection with the vertical line is a sign that the graph represents a office. On the other hand, the graph of the equations x = 5y2 and x2 + y2 = 81 fails the vertical line test since vertical lines pass through or intersect two points on their graphs.
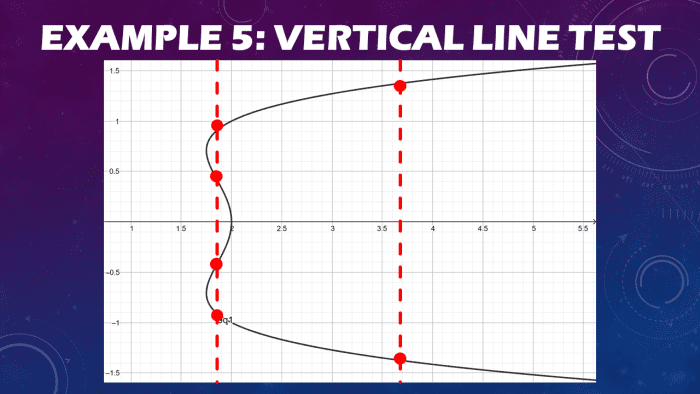
Example 5: Identifying if a Graph Is a Function
Sketch the graph of the function x = y4 - y2 + 2 and employ the vertical line test if it is a part.
Solution
Let united states offset the solution past tabulating all x and y points of the given equation. Solve for the values of y using random values of 10. Say, solve values of y at ten = ii, x = iii, x = five, and x = 10.
Sketch the graph of the given equation and perform the vertical line test. Equally you tin observe from the diagram shown beneath, no matter how many vertical lines you draw, they intersect the graph more than once.
Identifying if a Graph Is a Function
Final Reply
The graph of the equation x = y4 - yii + 2 fails the vertical line examination since two or more points of the function's graph intersect the vertical line.
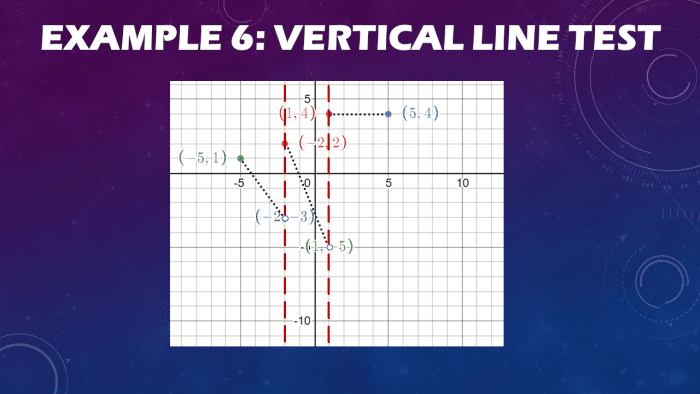
Example half dozen: Using the Vertical Line Test
Consider the graph shown with multiple points and identify if it is a function.
Using the Vertical Line Test
Solution
Permit us perform the vertical line test by drawing a vertical line to all the points shown in the graph. You can detect that no vertical lines pass through two points on the diagram twice or more. Ever note that points (-2, -3) and (1, -5) area open up points and are non on the graph. And then the vertical lines x = one and x = -ii laissez passer through just one spot of each line segment on the cartesian coordinate plane.
Concluding Reply
Since no vertical lines pass through the line segments twice, the blended graph is a relation or a function.
This content is accurate and true to the best of the author's cognition and is not meant to substitute for formal and individualized advice from a qualified professional.
© 2021 Ray
Vertical Line Test Math Definition,
Source: https://owlcation.com/stem/Vertical-Line-Test-Definition-and-Examples
Posted by: kongnoestringthe.blogspot.com


0 Response to "Vertical Line Test Math Definition"
Post a Comment